ENSM-SE
TP AXES PROCEDES
II - La cristallisation fractionnée
Plan
· A - La lecture de 2 types de diagrammes de phases
· B - Modéliser la cristallisation fractionnée
en utilisant les compositions des phases.
· C - Modéliser la cristallisation fractionnée
en utilisant les éléments en traces
· D - Travaux Pratiques
A - La lecture de 2 types de diagrammes de phases.
Les diagrammes de phases que
nous utilisons ici (Fig. 5a, diagrammes X vs. T), sont des représentations de
l’état du système dans l’espace de la composition (représentée par 2
constituants A et B selon X) et de la température T.
Aux hautes T° considérées, le système est généralement entièrement liquide (monophasé) quelque soit la concentration (f=2), et aux basses T° considérées, le système est entièrement solide; il peut alors être polyphasé si les constituants A et B représentent des corps purs non miscibles (f=1), ou monophasé si les corps représentés par A et B sont miscibles en toutes proportions (f=2, solutions solides = SS).
Entre ces deux états, initial et final, ces diagrammes nous montrent les deux domaines des compositions possibles pour le liquide et pour le solide. Ces deux domaines sont limités chacun par une courbe (f=1, composition fixée si T° fixée):
1. le liquidus limite en direction des basses températures le domaine des compositions possibles à l’état liquide;
2. le solidus, à l’inverse, limite en direction des hautes températures le domaine des compositions possibles à l’état solide.
Ces deux courbes sont toujours disjointes, sauf aux points d’abscisse A et B qui illustrent la cristallisation des corps purs représentés par A et B, et éventuellement en un point singulier de composition A/B défini, eutectique ou extremum (Fig. 5b, systèmes sans SS ; Fig5c, système à SS complètes). L’espace situé entre liquidus et solidus est donc un espace de composition impossible, tant pour le liquide que pour le solide.
Prenons l’exemple (Fig.5a)
d’un liquide L0 de composition initiale C0, à la
température T0. On constate qu’à
La composition de l’ensemble du système étant inchangée (C0), et le solide formé ayant une composition (CsT) différente de celle du liquide initial (C0), la composition nouvelle du liquide (ClT) peut être exprimée simplement en écrivant la relation de conservation de la masse:
q.CsT + (1-q).ClT = Cte (C0 dans notre exemple)
où q et 1-q sont respectivement les masses de solide et de liquide. La cristallisation d’un liquide peut donc être schématisée comme une suite d’événements, répétés comme suit (Fig. 5a):
1. A la température T1, le liquide en quantité = 1 et de composition C0 rencontre le liquidus, il n’est plus stable ;
2. il apparaît donc une masse q d’un solide de composition Cs0
3. la quantité de liquide disponible change (= 1-q) et sa composition nouvelle C1 diffère maintenant légèrement de sa composition au stade 0
4. la composition C1
est donc à nouveau au dessus du liquidus à la température T1, et
Arrêtons nous un instant sur la composition du solide formé à chaque incrément (Fig. 5a). Dans le cas des corps purs (A et B non miscibles), la composition du solide est constante, soit A soit B ; dans le cas des solutions solides, la composition du solide total est à chaque instant (chaque T°) celle du solidus. La cristallisation à l’équilibre impose donc, pour que le solide total formé ait la composition CsT, qu’il réagisse à chaque incrément avec le liquide, de composition ClT.
En résumé, lors de la cristallisation à l’équilibre d’un magma, la composition du liquide change au fur et à mesure que la quantité de liquide restant diminue, et celle du solide formé peut être soit fixe (cristallisation d’une phase minérale pure) soit variable (cristallisation d’une phase minérale solution solide).
Si dans nos diagrammes X vs. T le début de la cristallisation est toujours semblable, les modes de fin de cristallisation varient avec le type de phases minérales cristallisées :
1. avec la cristallisation d’une phase pure, le processus d’évolution s’arrête lorsque la composition du liquide atteint le liquidus de la seconde phase pure, à la température TE (eutectique = intersection des deux liquidus). Les deux phases A et B précipitent alors simultanément. Or le liquide est présent, donc f =3 et f=0 ; la température est donc bloquée à T = TE jusqu’à épuisement du liquide. Le solide final est alors constitué de deux phases minérales A et B dans des proportions massiques telles que la composition globale du solide soit C0, la composition du liquide initial.
2. avec la cristallisation d’une solution solide, le processus d’évolution s’arrête simplement lorsque tout le liquide a été progressivement épuisé. Le solide formé, monophasé, a rejoint progressivement la composition C0 du liquide initial. La température de fin de cristallisation est TFc, température du solidus pour la composition C0 ; contrairement à la cristallisation eutectique, elle ne marque pas de palier.
Si pour une raison quelconque, on peut considérer au cours du processus de cristallisation que le solide formé est soustrait du système (on parle de fraction soustraite, de "fractionnement"), le liquide L1 présent à cet instant prend valeur de liquide initial. Cela signifie que même si par la suite la cristallisation a lieu à l'équilibre, le solide final aura la composition du liquide L1 et non celle de L0, ce qui repousse la fin du processus et abaisse la température de fin de cristallisation TFC. Géologiquement, quatre processus de ségrégation de phases sont possibles à l’intérieur d’une chambre magmatique.
1. La vitesse de cristallisation est rapide et le solide formé n'a pas le temps d'atteindre l'équilibre avec le liquide. La conséquence en est le zonage de composition du solide, constitué d’enveloppes successives ; en outre, si le rééquilibrage du solide formé peut apparaître aisé au début du processus (liquide/solide >>1), il devient progressivement impossible avec la diminution de la quantité de liquide disponible ;
2. Le solide formé a une densité significativement différente du liquide : il est séparé par flottation, vers le haut ou vers le bas, il ne peut donc plus se rééquilibrer avec le liquide magmatique qui lui a donné naissance ;
3. La chambre magmatique, dans laquelle le liquide est en cours de cristallisation, est soumise à des gradients de température ; elle est donc parcourue de courants de convection capables d'accumuler les cristaux formés (comme des courants d'eau sont capables d'accumuler graviers ou galets) ;
4. La cristallisation d’une phase (à l’équilibre) peut créer un gradient de concentration tel, qu’au front de cristallisation, il va précipiter une nouvelle phase en remplacement de la précédente. Ce phénomène a toutes raisons d’être récursif. Il aboutira alors à une roche litée, comparable en tout point à des roches litées crées par flottation différentielle par exemple...
A ces processus de ségrégation minérale peuvent s’ajouter d’autres processus modificateurs de la composition des liquides magmatiques, qui interviennent pendant la remontée du magma dans la lithosphère. Deux d’entre eux sont importants :
1. L’assimilation de roches encaissantes, qui se produit lorsque l’encaissant réchauffé par le magma commence à fondre ; le produit de cette fusion partielle ou totale vient alors perturber la composition chimique du liquide magmatique
2. La contamination du liquide magmatique par la roche encaissante; il ne s’agit pas dans ce cas d’une fusion de l’encaissant mais d’un ensemble de réactions d’échange entre le magma (liquide) et son encaissant (solide)
On imagine bien que tous ces processus de ségrégation des phases précipitées, d’assimilation et de contamination vont créer, à partir d’un stock initial de liquide magmatique, des liquides différents (Tableau 3) et des roches variées (Fig. 6). Seule une analyse pétrographique poussée sera capable de faire la part des processus envisagés ici. Nous n’aborderons donc pas tous ces aspects du problème d’accumulation de phases (on parle de cumulats). Vous observerez d’une part des phases minérales zonées, témoignant d’un écart à l’équilibre lors de leur précipitation, et d’autre par la fusion partielle d’enclaves de granite (Fig. 7), arrachées par le basalte à son encaissant durant sa remontée, et plus ou moins assimilées.
B - Modéliser la cristallisation
fractionnée en utilisant les compositions des phases. 
La géochimie peut nous permettre
d'affirmer si les roches d’une famille ont quelques chances d'être cogénétiques, c'est à dire d'avoir eu le même liquide
initial ou des liquides initiaux très comparables. Une pile de laves comme
celle du Velay représente un échantillonnage de divers stades d’avancement d’un
processus de fractionnement qui avait lieu quelque part sous cette région à
cette époque. Chaque coulée correspond à un prélèvement effectué sur le système
en cours d’évolution. Elle peut correspondre soit au liquide de ce système,
soit à un mélange liquide + solide. De telles piles montrent généralement qu'il
n'y a pas nécessairement une progression régulière et unique de la composition
des laves dans le temps. En effet, les redites sont nombreuses, de même que les
discontinuités. Mais l’ensemble des compositions des coulées peut parfaitement
représenter un processus de fractionnement unique (ou un ensemble de processus
similaires). Les redites peuvent ainsi être dues à des remplissages itératifs
dans une chambre magmatique en cours de fractionnement. Les discontinuités dans
l’évolution de la composition reflètent en premier lieu le caractère discontinu
(à l’échelle géologique, 102-104 ans) des éruptions, mais
leur origine peut être variée ; citons pour mémoire, l’évolution de la
viscosité et de
La géochimie s’intéresse à la composition des roches, qu’elle décrit dans l’espace à n dimensions des composants : on considère généralement 10 composants majeurs présents en quantité >0.01% en plus de H2O : SiO2, Al2O3, FeO et/ou Fe2O3, MnO, MgO, CaO, Na2O, K2O, TiO2, et P2O5 (Tableau 3). Le nombre des éléments en traces varie considérablement, en fonctiona du type de processus étudié, et des moyens techniques d’analyse. En fait, leur nombre n’est limité que par le nombre des cases du tableau périodique, la stabilité des éléments, et bien sûr les difficulté à les mesurer précisément . Ils sont généralement exprimés en ppm.
Dans un tel espace, un processus donné de cristallisation fractionnée se traduira par le mode de distribution des produits qu’il a engendré (liquides et cumulats) depuis le liquide initial jusqu’au liquide terminal. Les liquides seront distribués le long d’un même chemin, rectiligne, curviligne, voir même en ligne brisée (Fig. 8). Inversement, si dans la collection d’échantillons auxquels on s’intéresse il existe plusieurs processus différents de fractionnement, on obtiendra une distribution selon plusieurs directions, avec des courbures différentes, ou avec des brisures différentes. Si deux processus de fractionnement, similaires ou non, n’ont pas le même point de départ, cela signifie vraisemblablement qu’ils ont agit sur des liquides initiaux différents, et par conséquent, qu’il y avait des processus de fusion (mantellique ou crustale) différents à l’origine de ces liquides. Une bonne connaissance de ces liquides initiaux permet ainsi d’espérer que l’on pourra reconnaître les conditions de la fusion partielle qui leur a donné naissance.
On peut encore tenter d'identifier des processus qui ont pu affecter la composition de ces liquides depuis leur stade d'extraction jusqu'au début de leur fractionnement, et accéder ainsi aux phénomènes qui gouvernent l'évolution du manteau supérieur et de la croûte terrestre.
Le premier pas de l'analyse d'un processus de fractionnement est bien évidemment la caractérisation des solides formés lors de la cristallisation du liquide. Les phases essentielles qui peuvent être présentes au liquidus d'une composition de liquide initial (composition basaltique) sont:
·
olivine
ol (Mg,Fe)2[SiO4]
·
orthopyroxene
opx (Mg,Fe)2[Si2O6]
· clinopyroxene cpx Ca(Mg,Fe)[Si2O6] Na(Al-Fe3+)[Si2O6]
· plagioclase (feldspath) plg Ca[Si2Al2O8] Na[Si3AlO8]
· apatite ap Ca5 (PO4)3 (OH, F, Cl )
·
oxydes Ti Fe
ox FeTiO3
FeO-Fe2O3
La nature des phases
présentes et l'ordre dans lequel elles apparaissent et/ou disparaissent est
variable d'une région volcanique à une autre. Cela dépend en particulier de la
composition de départ (liquide initial) et de
Plus tard, d’autres phases minérales apparaîtront ou non:
· amphibole hn Ca5 (Mg,Fe)3 [Si8O22] (OH)2 NaCa(Mg-Fe)3(Al-Fe3+)2[Si6Al2O22] (OH)2
· biotite bi K2 (Mg,Fe)6 [Si6Al2O20] (OH)4.
· Feldspath Na-K fK Na[Si3AlO8] K[Si3AlO8]
L’observation des phases cristallisées à partir du liquide initial, et leur ordre d'apparition et de disparition sont les contraintes fondamentales que nous pourrons appliquer à un modèle géochimique de fractionnement comme suit :
1. Dans un espace de composition donné, connaissant les compositions du liquide initial L0 et du premier solide formé S1, on peut calculer la composition du liquide L1 en équilibre avec le solide S1, le liquide L0 représente le barycentre du système S1-L1 (Fig. 9)
2. Si la composition du solide formé est constante, et si la cristallisation a lieu à l’équilibre, la loi reste vraie quelque soit la quantité de solide formé. La distance L0-L1 va s’accroître avec la quantité de solide formé, et inversement, la quantité de liquide va décroître, mais L0 restera le barycentre du système.
3. Par contre si le fractionnement du solide S1 est total, tout le solide formé est exclus du système, qui se réduit alors à L1. On doit alors considérer L1 comme le nouveau barycentre du système en cours de cristallisation. Dans tous les cas intermédiaires, correspondant à un fractionnement partiel du solide s1, le nouveau barycentre du système sera situé quelque part entre L0 et L1, au prorata du solide soustrait.
Donc, quelque soit le taux de fractionnement du solide, si sa composition reste constante dans l’espace de composition considéré, ou plus exactement si le rapport des concentrations dans cet espace reste constant, la distribution des liquides successifs constituera une droite passant par L0 et S1. Si chacune des phases en présence présentait une composition constante, le modèle serait donc très simple. Hélas la plupart des phases en présence sont des solutions solides, Fe-Mg pour l’olivine, l’orthopyroxène et le clinopyroxène, Na-Ca +Si-Al pour le plagioclase. Il faut non seulement reconnaître la présence des phases, mais il faut aussi connaître leur composition, car elle évolue, plus ou moins rapidement avec le taux de cristallisation du liquide. Dans le cadre de ce TP, nous n'aurons pas à tenir compte de toute cette complexité.
C - Modéliser la cristallisation
fractionnée en utilisant les éléments en traces 
La loi de Rayleigh
Avec les phases minérales nous avons vu comment reconstituer les étapes de la cristallisation (fractionnée ou non) en utilisant les constituants majeurs du système. A leur côté, nombre d'éléments sont présents en quantités infinitésimales (« en traces ») dans le liquide magmatique. Ils sont plus ou moins capables de se substituer aux éléments majeurs dans les phases qui cristallisent. Ils peuvent aussi en être tout à fait incapables. Nous allons pouvoir utiliser cette affinité variable pour les espèces minérales, comme des marqueurs très fins des processus de cristallisation du magma.
La compréhension du comportement de tel ou tel élément vis à vis de telle ou telle phase passe par une bonne connaissance:
1. d’une part des caractéristiques chimiques de l’élément, rayon ionique, valence(s)...
2. d’autre part des propriétés cristallochimiques des phases minérales, en particulier des types de sites et de leur taille.
Arrêtons-nous un instant sur quelques éléments bien typés:
Ni, de rayon ionique proche de celui du Mg et de valence 2 se substitue aisément à celui-ci dans l’olivine, où le Mg occupe un site octaédrique. La cristallisation de l’olivine est donc marquée par un appauvrissement du liquide en Ni. Le coefficient de partage du Ni entre l’olivine et le liquide
(Kdol-liqNi) = ([Ol]/[Liq])Ni est supérieur à 1 (tableau 4)
Cr, trivalent, ne peut entrer dans l’olivine. Par contre il entre aisément dans le réseau du clinopyroxène, capable de substitutions Al3+ et Fe3+, donc:
(KdOl-liqCr) = ([Ol]/[Liq])Cr inférieur à 1
(KdCpx-liqCr) = ([Cpx]/[Liq])Cr est supérieur à 1
Si l’olivine est seule présente au liquidus, le liquide s’enrichira en Cr, puis lorsque le Cpx commencera à cristalliser, la teneur en Cr du liquide commencera à chuter.
Eu2+, entre aisément avec le Sr dans le réseau de plagioclase en remplacement du Ca.
Y, comme les Terres Rares lourdes, entre volontiers dans le réseau de l’apatite,
Nb et V, présentent comme le Cr une forte affinité pour les oxydes de fer, la magnétite ou l’ilménite.
Certains éléments, en particulier le Zr, n’ont qu’une faible affinité pour toutes ces phases minérales hôtes. Il sont dits hygromagmatophiles (qui aime les volatils et le magma) ou incompatibles (avec les solides formés). La concentration en Zr croît jusqu’à apparition d’une phase particulière, le zircon (Zr[SiO4]). Le Nb peut lui aussi être considéré comme tel si la magnétite n’est pas fortement cumulée, mais il ne formera pas de minéral de Nb (sauf cas particuliers). Il attendra alors la cristallisation de la biotite pour devenir compatible. Le comportement général des incompatibles est lié soit à leur très grosse taille (LILE= large ion lithophile element), ou à leur charge élevée (HFSE= high field strength element), ou bien encore à une forte tendance à constituer des anions complexes dans le liquide, qui ne peuvent être intégrés dans les structures silicatées. La notion de lithophilie représente la tendance de ces éléments à se concentrer dans la lithosphère au détriment du manteau. On peut replacer ici des éléments évoqués plus avant, U, Th, K.
Eu2+ excepté, les lanthanides sont trivalents et ont un rayon ionique voisin. Toutefois, la variation de taille de ce rayon, du La au Lu, est suffisante pour que les processus naturels puissent fractionner chaque lanthanide différemment du précédent et du suivant. Cette variation régulière de leur comportement en fait des marqueurs très prisés des géochimistes.
Du fait des différences chimiques qu’ils présentent vis à vis les cations présents dans les espèces minérales hôtes, les éléments en traces sont loin de se substituer idéalement à ces cations ; ces composants en solution peuvent en effet interagir fortement avec les autres composants majeurs et les écarts à la linéarité de la loi de Raoult deviennent très importants (Fig. 10). Toutefois, puisque nous sommes (par définition) dans le domaine des basses concentrations, une variation de concentration de ces traces n’affectera pas significativement le comportement de la solution hôte. Les coefficients d’activité des éléments en traces vis à vis des solutions minérales restent donc strictement proportionnels aux concentrations (Loi de Henry, par exemple : aNbliq = kNbliq . XNbliq).
L’application de la loi de Henry à des phases en équilibre (égalité des potentiels chimiques, pour l’élément i, miliquide = m IOlivine par exemple), implique que le rapport des concentrations en masse (XIOl / XIliq) de l’élément considéré entre les deux phases est constant ; en effet :
on a m0Iliq + RT ln a Iliq = m0IOl + RT ln a IOl
avec aIliq = kIliq
. XIliq
on a ![]()
et donc 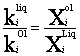 = D
= D
« D », le coefficient de partage apparent du Nb entre le liquide et l’olivine, est constant dans les conditions P et T° de l’équilibre seulement. Comme les constantes d’équilibre, les coefficients de partage sont donc dépendants de P et de T°. Par ailleurs, les variations de composition des minéraux (l’olivine dans notre exemple), avec la composition du liquide qui leur donne naissance, sont aussi susceptibles d’en modifier la valeur. Un coefficient de partage donné n’a donc aucune signification universelle ; au cours d’un processus de cristallisation fractionnée par exemple, on définira plusieurs valeurs du coefficient de partage (celui du La entre le plagioclase et le liquide par exemple), une pour les basaltes (SiO2 45-55%), une pour les andésites (SiO2 55-65%) et une pour les rhyolites (SiO2 45-55%). Il est à noter que pour les éléments hygromagmatophiles ces valeurs vont croissant, témoignant de l’affinité croissante de ces éléments pour les phases minérales (Fig.11) . Par souci de simplification, les valeurs que nous vous donnons (tableau 4) sont uniques ; elles sont strictement indicatives et vous permettront d’évaluer qualitativement le comportement des éléments dans le processus de cristallisation fractionnée.
Considérons un réservoir de
liquide magmatique, contenant n moles de constituants, dont x moles de l’élément
i. La fraction molaire initiale de i dans le liquide est.![]() = x/n
= x/n
Dès lors qu’un minéral
cristallise et se trouve fractionné, il a consommé (il est soustrait du
système) dn moles de constituants et dx moles de i.
Il reste dans le système (n-dn) moles de constituants
dont (x-dx) moles de i. Les fractions molaires de i
dans le minéral et le liquide sont alors respectivement
![]() =
= ![]() et
et
![]() =
= ![]()
Et le coefficient de partage s’écrit
![]() /
/![]()
donc ![]() =
= ![]()
Si l’on néglige![]() =
=![]()
et ![]()
en
dérivant par rapport à n, ![]() = n .
= n . ![]() +
+ ![]()
On peut donc écrire le
coefficient de partage D tel que ![]() = n
.
= n
. ![]() +
+ ![]()
Que l’on peut réarranger en
![]()
L’intégration de cette
équation,
entre ![]() la concentration initiale de l’élément i et
la concentration initiale de l’élément i et
![]() sa concentration instantanée
sa concentration instantanée
et entre n0 et n les quantités initiale et finale de liquide, nous donne le changement total de concentration:
On a donc
![]()
et
![]()
On appelle![]() , la fraction de la masse du liquide par rapport à la masse
totale initiale, le degré de fractionnement,
, la fraction de la masse du liquide par rapport à la masse
totale initiale, le degré de fractionnement,
et l’on écrit :
![]() loi de Rayleigh
loi de Rayleigh
Nous
ne détaillerons pas ici le cas d’une cristallisation à l’équilibre, qui
impose un rééquilibrage permanent du solide formé avec le liquide. Ce mode d’évolution
est théoriquement possible mais très peu réaliste, compte tenu des vitesses de
diffusion intracristalline, voir même de diffusion
dans le liquide. L’expression de l’évolution de la concentration en fonction du
degré de fractionnement est alors de la forme suivante :
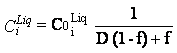
D, le coefficient de partage global instantané de l’élément i entre le solide formé et le liquide restant peut être exprimé comme la somme des coefficients de partage de l’élément i entre le liquide et toutes les espèces minérales qui cristallisent, tel que : D = S1-n (Kd min-liqi) * Fm, où n est le nombre de minéraux constituant le solide, et Fm est la fraction du minéral m dans le solide formé.
L’influence de D sur l’évolution de la concentration est donnée dans la figure 12. On remarquera que même pour une valeur nulle de D, l’évolution de la concentration dans le liquide ne devient importante et rapide qu’à des stades avancés de fractionnement. Inversement, si D>>1, l’appauvrissement du liquide est extrêmement brutal au départ.
Le comportement des éléments incompatibles, très utiles au géologue, (D<<1) se réduira à deux propriétés essentielles:
1 - l’enrichissement du liquide au cours du processus
2 - l’existence pour un processus de fractionnement donné, de corrélations linéaires entre ces éléments pris deux à deux
En effet, si D est petit devant 1, la loi de Rayleigh s’écrit
Ci = C0i*1/f
Pour deux éléments, on aura:
C1 = C01 /C02 * C2
D -
Travaux Pratiques 
Vous ne devez pas oublier que ce TP a pour objectif l’utilisation de méthodes d’acquisition des données pour tracer un process, en conséquence :
1. vous ferez des observations et mesures à diverses échelles, cartes, terrain, échantillon, microscopie optique et électronique (MEB) ;
2. vous acquérrez et/ou disposerez de données physico-chimiques, diffractogrammes (XRD), analyses de minéraux (MEB), analyses chimiques de roches (XRF, ICP) ;
vous devrez ensuite tester la pertinence de ces différents modes d’observation et de caractérisation dans le traçage de la cristallisation fractionnée :
1. en vous esseyant à reconnaître le ou les processus de fractionnement dans une population de roches dont nous vous fournissons des échantillons et les analyses
2. en illustrant et
argumentant votre approche du problème dans un mini rapport