ENSM-SE / processus naturels / terre_ronde

CHAPITRE 1

Evacuer la Chaleur de la Planète

retour

B- La Convection

Dans ce cas, la matière elle-même est transportée, entre deux couches limites au sein desquelles la chaleur est évacuée par conduction. La figure 1 représente une couche fluide, chauffée par-dessous. Les températures de surface et du fond sont respectivement T₀ et T₀+DT. Si une goutte de ce fluide quitte le fond et s'élève de la hauteur dz, suffisamment vite pour ne pas échanger de chaleur avec son environnement, sa décompression adiabatique (a, coefficient de dilatation thermique) impliquera une baisse de température telle que

dT = (gaT/C_p)dz où

(gaT/C_p) représente le gradient adiabatique grad T_ad.

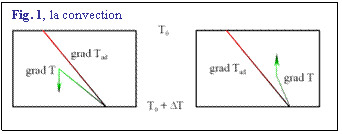Si le gradient de température supposé linéaire dans la couche fluide est plus petit que le gradient adiabatique (sous adiabatique, grad T< grad T_ad , à gauche dans la figure), la goutte sera plus froide que son environnement, donc plus dense. Elle redescendra et la convection avorte. Inversement si le gradient de T° est super adiabatique, grad T<grad T_ad, à droite dans la figure, la goutte est plus chaude et plus légère que son environnement, la convection est amorcée. Elle tend donc à monter vers la surface. S'il n'y a pas d'échange de chaleur avec l'environnement le gradient de T° se rapproche du gradient adiabatique.

On pourrait en déduire que l'existence d'un gradient de température suffit pour entraîner un écoulement convectif. En réalité, pour que le régime convectif s'amorce, le gradient de température doit atteindre un certain seuil. En effet, deux facteurs jouent un rôle important pour le mouvement d'une goutte de fluide et s’opposent :

1) la poussée d’Archimède (dirigée vers le haut) ;

2) la traînée visqueuse (force de frottements) dirigée dans le sens opposé au mouvement. Sa grandeur dépend de la viscosité du fluide.

Donc, il n' y a pas de mouvement tant que la traînée visqueuse est égale au 2^d facteur, la poussée d'Archimède.

Pour que la convection fonctionne, il faut donc une poussée d'Archimède suffisante, c’est à dire:

1 - une pesanteur g (m.s^-2), forte;

2 - un coefficient de dilatation thermique a (K^-1), élevé;

3 - un gradient de température élevé, donc DT (°K) élevé;

4 - une hauteur fluide z (m), élevée (l'écart de température avec l'environnement augmente avec z)

5 - une production interne de chaleur, Q, n'est pas indispensable, mais favorise la convection;

et une faible dissipation, c’est à dire:

6 - une diffusivité K (m².s^-1), et une conductivité k (W.m^-1.K^-1) thermiques faibles, donc une chaleur spécifique volumique importante C_p (J.K^-1.m^-3);

7 - une viscosité cinématique du fluide ν (m².s^-1), basse ; avec ν = h /r (h, viscosité dynamique).

On exprime l'ensemble de ces paramètres à travers un nombre sans dimension, dit Nombre de Rayleigh,. indépendant des détails du système considéré, et qui, pour une couche horizontale chauffée par-dessous, sera de la forme

Ra = gaz³DT / νK

et pour une sphère chauffée de l'intérieur (Q), sera de la forme:

Ra = gaQ z⁵DT / νK

Dans le cas où la couche de fluide est comprise entre deux plans infinis, des calculs théoriques montrent que le nombre de Rayleigh critique a une valeur de 1708.Des expériences menées par P. Silveston et E. Koschmieder laissent prévoir également que Ra est de l’ordre de 1700 ± 50.

Dans une couche horizontale simple comme la précédente, le fluide devient instable et convecte pour une valeur critique de Ra = 667.

La viscosité est un paramètre essentiel de la convection, quelques rappels :

1 - Un fluide parfait, de viscosité nulle, est caractérisé par un module élastique nul, m = 0. Toute contrainte de cisaillement engendre une déformation irréversible, il coule donc parfaitement. Un fluide visqueux au contraire résiste à l'écoulement. Donc, pour maintenir l'écoulement à vitesse de déformation (e) constante, de/dt = cte, il faut appliquer une contrainte de cisaillement s. La viscosité, h, est de la forme de s/e.

1 - Un solide supporte la déformation de manière élastique en dessous d'une certaine valeur, et une déformation irréversible au-delà. Une contrainte quelconque, appliquée longtemps, provoque une déformation qui croît avec le temps. Le solide s'écoule comme un liquide, on dit qu’il flue, et sa viscosité h est encore définie par le rapport s/e, où e est la vitesse de fluage. Le modèle du corps de Maxwell (Fig.2) rend compte de ce comportement, en écrivant que la déformation totale est égale à la déformation élastique (s/m) plus la déformation visqueuse:

e = (s/m) + s/hdt

Le temps de relaxation d'un tel corps est égal à t,= s/h

Pour une contrainte appliquée pendant un temps inférieur au temps de relaxation, le corps a une réponse élastique, alors que pour une contrainte appliquée pendant un temps très supérieur, la réponse sera un écoulement visqueux. Pour le manteau terrestre, on sait que :

1 - la viscosité h est estimée de l'ordre de 10²² poises (ou Pascal.seconde);

2 - le module élastique de cisaillement m est estimé de l'ordre de 70 G.Pascal.

D'où l'on tire un temps de relaxation, qui pour le manteau terrestre est de 450 ans, valeur tout à fait compatible avec la convection à l'échelle des temps géologiques. On estime à cet égard qu'une cellule convective est parcourue en 10⁶ années. La valeur du nombre de Rayleigh obtenue pour la Terre est de l'ordre de 10⁸. Elle est donc très supérieure à la valeur critique.

Pour une sphère en rotation rapide comme la Terre, et un fluide à faible viscosité comme le fer liquide du noyau, la force de Coriolis devient significative. Busse a montré que la circulation convective prend alors la forme de colonnes étroites parallèles à l’axe de rotation de la sphère.

La formulation de la théorie des plaques, en combinant la géophysique et la dérive des continents de Wegener, a permis d'avoir un regard à l'échelle de la planète sur les phénomènes géologiques. Il est maintenant admis que le mouvement perceptible en surface des plaques lithosphériques rigides de la croûte terrestre n'est que le reflet de mouvements convectifs intéressant tout le manteau. Celui-ci est un solide à l'échelle de temps des phénomènes acoustiques qui nous permettent de l'ausculter (cf. Chp. 3.B), mais un fluide à l'échelle des temps géologiques. Si l'observation directe des parties profondes de cette circulation nous est hélas impossible, il nous reste bien sur Jules Verne, mais surtout les modèles dérivés des études de séismologie (cf. Chp. 3B et 4.C).

Nous avons exprimé plus avant que la convection dans le manteau est contrôlée par le nombre de Rayleigh, qui décrit la vigueur de la convection. Dans les modèles terrestres, si l’on peut considérer que le plancher océanique constitue la surface supérieure des cellules convectives du manteau terrestre (cf. Chp. 4.E.2 lithosphère océanique), il n’en est pas de même des continents. En effet, la lithosphère continentale échappe presque complètement au recyclage convectif (Chp. 4.E.1 lithosphère continentale). Elle est certes mobile à la surface de la Terre, mais elle reste à la surface. En outre, elle est quasi exclusivement solide, et ne peut donc transférer la chaleur apportée à sa surface inférieure par la convection mantellique que par conduction. Bien identifiée par la sismique ,les anglo-saxon donne à cette « seismic-lithosphere » le nom de LID (=couvercle). Elle agit comme un bouclier thermique, dont l´effet plus ou moins isolant est introduit dans les modèles de convection mantellique (e.g. S. Labrosse, C. Jaupart et C. Grigné) par un second nombre sans dimension, le nombre de Biot. Le nombre de Biot s´écrit : B=(k_c d_m)/(k_m d_c), où k_c et k_m sont les conductivités thermiques respectivement du continent et du manteau, et d_c et d_m sont leurs épaisseurs. Utilisé dans les calculs de transfert thermique en phase transitoire, il compare la résistance au transfert thermique à l'intérieur du volume d’un corps (ici le continent) à celle de la surface du corps considéré (ici l’interface entre le continent et le manteau situé au dessous).

On peut montrer que le flux de chaleur sortant du manteau sous le continent est proportionnel à B.T_i, où T_i est la température à l´interface entre les deux milieux. Un nombre de Biot élevé, correspondant à une épaisseur du continent d_c faible ou à une conductivité thermique k_c élevée, implique un effet isolant très faible de la part du continent. A l´inverse, un nombre de Biot faible correspond à une forte épaisseur du continent ou à une conductivité faible, et donc, à un fort effet 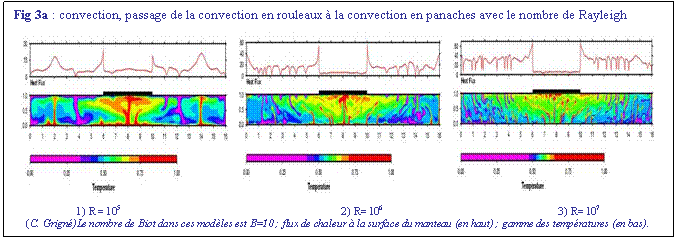isolant :

1 - Pour un continent immobile, la convection d'un fluide sous un couvercle conductif se traduit toujours par le développement d´une zone de remontée chaude centrée sous le couvercle-continent, quel que soit son nombre de Biot. En outre la largeur des cellules de convection augmente par rapport à celles du modèle de convection semblable sans couvercle, et leur nombre décroît (2 au lieu de 4). En fonction de la vigueur de la convection, les modèles suggèrent que l’on passe d’une convection en rouleaux correspondant à un écoulement lent et laminaire (Fig. 3a1, Nombre de Rayleigh faible 10⁵) à un modèle de gouttes séparées de fluide chaud (panaches) plus rapides que leur environnement, qui traduisent la turbulence du milieu (fig. 3a2-3a3, Nombre de Rayleigh moyen et fort, respectivement 10⁶ et 10⁷). L´écoulement peut atteindre un état stationnaire dans le mode lent, mais pas dans le mode rapide. Le second enseignement de ces modèles de circulation mantellique est que la largeur des cellules convectives est corrélée d’une part au nombre de Rayleigh (fig. 3a) et d’autre part à la taille du couvercle (fig.  3b).

2 - Pour un continent mobile, au stade initial, le continent est immobile. Dans un premier temps la divergence installée sous le continent par les ascendants mantelliques provoque la dérive du continent jusqu’au droit d’un descendant mantellique, point de convergence des cellules convectives. L’effet de bouclier thermique du continent devenu stable se traduit alors par une modification complète de la distribution des cellules, jusqu’à apparition d’une nouvelle divergence sous le continent. Si la taille du continent influe directement sur la taille des cellules convectives (continent fixe de petite taille, continent fixe de grande taille), on observe en outre une évolution très nette de la largeur des cellules convectives avec le déplacement du continent. Initialement larges tant que le continent reste immobile, elles sont rapidement remplacées par un système de cellules de longueur d’onde bien plus petite dès lors que le continent est mobile. L’effet cumulatif de bouclier (qui se traduit par l’allongement des cellules) disparaît avec la mobilité de ce dernier.

Si de tels modèles ont l’immense avantage de visualiser le phénomène convectif, ils ne permettent pas encore de rendre compte de la complexité du phénomène terrestre.

La géologie nous enseigne par exemple que le rift océanique (qui correspond à un ascendant mantellique) peut se poursuivre à travers le continent, et qu’il peut entraîner sa rupture (e.g. la ride Indienne qui se poursuit en Mer Rouge et dans le rift Est Africain). Le bouclier continental afro-arabique apparaît ici passif, fragilisé et dilacéré par la convection mantellique. Quelle est l’influence réelle de la surchauffe continentale sur la position des ascendants mantelliques ? La position des continents détermine-elle celle des panaches ascendants ? Nombre de géologues discutent encore le mouvement relatif des plaques et suggèrent qu’il résulte de la traction par les plaques subductées. La question a-t-elle un sens ? Nous verrons aux chapitres 3 et 4 que la distinction d’un manteau inférieur et d’un manteau supérieur vient compliquer encore la circulation dans le manteau, et que les interactions entre le manteau et le noyau sont aussi un facteur à prendre en compte.

C- L’advection

La convection est le mode premier du transfert de chaleur dans le manteau, ce qui n’interdit pas bien entendu qu’une partie de la chaleur du manteau est aussi transmise vers l’extérieur par conduction. Nous venons de voir que la lithosphère, partie rigide de la Terre (et en particulier la lithosphère continentale), ne permet pas la convection, et donc que le transfert la chaleur s’y effectue par conduction.

Mais dans la lithosphère, le volcanisme en provenance du manteau transporte lui aussi de la chaleur vers la surface, sous forme de matériau chaud qui reste stocké dans la lithosphère. Le volcanisme représente ainsi une perte de chaleur qui ne s’effectue ni par conduction ni par convection, mais par advection.

haut

retour

début

précédent chapitre suivant

( Conduction ) précédente page suivante ( Bilan Energies )

Plan