ENSM-SE / processus naturels / terre_ronde
CHAPITRE 2
Les météorites
retour
3 - le fractionnement isotopique des espèces chimiques
Nous avons vu jusque là un ensemble de processus capables de fractionner les éléments chimiques. Mais les processus physico-chimiques sont aussi capables de fractionner les différentes espèces isotopiques d’un composé engagé dans ces processus. De tels fractionnements isotopiques des espèces chimiques constituent un outil extrêmement performant pour tracer les processus géochimiques, que le lecteur retrouvera en des endroits très divers de ce polycopié. On s’intéresse ici aux isotopes stables (non radioactifs et non radiogéniques), dont la quantité dans un réservoir donné n’évolue pas par radioactivité, mais par déplacement vers ou depuis un autre réservoir au cours de processus physico-chimiques. Nous n’aborderons pas ici le cas des isotopes radioactifs d’éléments pères, dont la décroissance naturelle au cours du temps provoque la croissance naturelle d’éléments fils dits radiogéniques, couples classiquement utilisés en datation.
Nous décrirons ici sommairement les principes du fractionnement isotopique d’isotopes stables, en reprenant le manuel « Géologie isotopique » de C. Allègre, 2005, partant de l’exemple de l’eau, constituée de deux H et un O. Ce composé comprend ainsi diverses molécules, à base de 1H (l’hydrogène léger, H), de 2H et 3H (les hydrogènes lourds, Deutérium, D, et Tritium, T), et de trois isotopes de l’oxygène, 18O, 17O, 16O du lourd au léger . Pour molécules les plus courantes, nous aurons donc :
1 - H218O (2.2%) ; H217O
(0.5%) ; H216O
(97%) ;
2 - D218O ; D217O ; D216O ;
3 - DH18O ; DH17O ; DH16O (0.3%) ;
Notons que quatre espèces isotopiques seulement sont > 0.1%, dont une qui domine largement.
On peut donc considérer que tout composé constitué d’éléments présentant des isotopes sera, en quelque sorte, marqué par un ensemble de rapports isotopiques caractéristiques. Si un tel composé est engagé dans un processus, chimique ou physique, les différences de masse entre les isotopes aura pour effet de fractionner les espèces légères et lourdes de ce composé. Quatre types de fractionnement peuvent se produire :
1 -
 fractionnements d’équilibre, 1)
chimique 2) physique ;
fractionnements d’équilibre, 1)
chimique 2) physique ;
2 - fractionnements cinétiques, 3) transport 4) réaction.
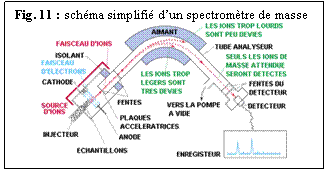
Le spectromètre de masse, outil qui mesure simultanément les concentrations isotopiques en séparant spatialement les espèces différentes par application de la force centrifuge lors de leur déplacement (Fig. 11), permet d’accéder avec précision à ces rapports isotopiques.
Aussi
utilise-t-on communément les variations de ces rapports, en les comparant à
ceux d’une substance prise en référence. Il s’agira d’un carbonate de calcium
CaCO3 référence (bélemnite
[1]
de
d = [(REch
- Rstd) / Rstd].103
On appellera ainsi d18O d’une eau (prononcer delta O18), l’écart entre la mesure du rapport 18O/17O
faite sur un échantillon d’eau et la
valeur standard SMOW de ce rapport :
d18O = [(18O/16OEch - 18O/16OSMOW)
/ 18O/16OSMOW].103
a- Le fractionnement d’équilibre chimique
Voyons la réaction d’échange 18Oó16O suivante :
Si18O2 + 2H216O
ó Si16O2 + 2H218O
Comme toute réaction chimique elle admet pour constante d’équilibre (loi d’action de masse) thermo dépendante (Ln K = a’ +b’/T +c’/T2)
K(T)
= (Si16O2).(H218O)2 /
(Si18O2).( H216O)2
H. Urey a montré (mécanique statistique quantique) que si K est bien voisine de 1, elle est néanmoins différente de 1, et pour une réaction d’échange d’isotopes entre deux composés, A et B, constitués de deux isotopes is1 et is2 d’un élément commun aux deux composés,
aAis1 + bBis2 ó aAis2 + bBis1
Selon la thermodynamique statistique, la constante d’équilibre s’écrit :
K(T) = [Q(Ais2)/Q(Ais1)]a
. [Q(Bis1)/Q(Bis2)]b
Où les fonctions Q(Ais1), Q(Ais2) …etc., sont appelées fonctions de partition des différentes molécules isotopiques.
Avec, pour chaque composé, deux molécules (1 et 2), constituées respectivement des isotopes is1 et is2:
M1 et M2, les 2 masses des deux molécules
s1 et s2, leurs nombres de symétrie ;
E1 et E2, leurs niveaux d’énergie (rotation-vibration)
I1 et I2, leurs moments d’inertie
Le rapport des fonctions de partition pour cette molécule
Q2/Q1=
(s1/s2).(I1/I2).(M2/M1)3/2.[S exp(E2/kT)
/.[S exp(E1/kT)]
Fait apparaître deux caractères essentiels de la réaction d’échange isotopique:
1 - Le fractionnement entre deux espèces isotopiques est proportionnel au rapport des masses de ces espèces ;
2 -
La thermo dépendance de K, plus
On définit le coefficient de fractionnement isotopique chimique a, dépendant de la température,
aAB = (Ais2 / Ais1) / (Bis2
/ Bis1)
Les coefficients a et K sont liés par la relation
a = K1/n
ou n est le nombre d’atomes échangeables dans cet équilibre. Dans le cas de l’échange des isotopes 16 et 18 de l’oxygène entre une espèce de SiO2 (e.g. Quartz) et de l’eau, le nombre d’atomes échangeables est n = 2.
b- Le fractionnement d’équilibre physique
Un fractionnement isotopique intervient aussi lors des changements de phase d’un composé. Ainsi, pour l’eau lors de l’évaporation (eg. au dessus des océans) et lors de la précipitation (pluie ou neige), on peut s’attendre à un fractionnement de l’oxygène, entre 18O et 16O de masses très différentes, mais aussi à un fractionnement de l’hydrogène entre 1H et D, lors de l’évaporation (eg. au dessus des océans) et lors de la précipitation (pluie ou neige).
Continuant notre lecture de l’ouvrage de C. Allègre, nous définirons la pression partielle Pgaz d’une espèce gazeuse présente à la concentration Xgaz dans un mélange comme :
Pgaz= Ptotale . Xgaz
Pour des espèces d’eau différentes par leurs isotopes de l’oxygène, lors de l’évaporation de l’eau liquide, l’équilibre liquide ó gaz conduit à écrire (loi de Henry) :
P(H216O)
= Ptotale . Xgaz(H216O),
P(H218O)
= Ptotale . Xgaz(H218O),
et considérant le mélange comme un gaz parfait, avec P°, pression de vapeur saturante :
P(H216O)
= Xliq (H216O) . P°(H216O)
P(H218O)
= Xliq (H218O) . P°(H218O)
Le coefficient d’échange a lors de la vaporisation ne sera donc dépendant des pressions de vapeur saturante des deux espèces, il sera de la forme
avap-liq = P°(H218O) / P°(H216O)
Or le liquide le plus dense est le moins volatil, donc
avap-liq <1
Dans le cas de l’eau pris en
exemple, les coefficients de fractionnement, à
a(18O) =0.9911 ; a(D)
=0.9180
Le fractionnement
à
c- Le fractionnement cinétique de transport
Lorsqu’un processus engage un phénomène de transport, l’énergie utilisée pour ce transport va ce traduire par des différence de la vitesse acquise par les différents composés transportés en fonction de leur masse, en respect de la loi E = ½ mv2 Pour deux espèces isotopiques 1 et 2 d’un composé, les vitesses v1 et v2, auxquelles les molécules isotopiques 1 et 2 se déplacent sont fonction de leurs masses m1 et m2.
Le coefficient de fractionnement isotopique cinétique de transport, est donc de la même forme que le rapport des vitesses v1/v2 = (m2/m1)1/2 :
a leger-loud= vleger/vlourd
= (mlourd/mléger)1/2
Lors du déplacement d’une masse d’air par exemple, les molécules de dioxygène 16O2 sont fractionnées par rapport aux molécules un peu plus lourdes de 17O2, enrichissant
l’air transporté comme suit :
a (16O2-17O2)
= (2x17 / 2x16)1/2 = 1.03078
Contrairement aux précédents coefficients de fractionnement isotopique, celui de cinétique de transport est indépendant de la température ; il ne dépend que du rapport des masses des molécules isotopiques.
d- Le fractionnement cinétique de réaction
Les vitesses de réaction de deux molécules isotopiques d’un composé donné dans une réaction chimique ne sont pas non plus exactement les mêmes. Les molécules légères sont un peu plus réactives, d’une part parce qu’elles se déplacent plus vite et accroissent ainsi leur nombre de collisions avec les autres réactifs, d’autre part parce qu’elles sont un peu moins stables que leurs sœurs lourdes. C. Allègre prend ici l’exemple de l’oxygène dans la réaction d’oxydation du carbone C + O2 ® CO2 ; en raison des abondances naturelles des isotopes de l’oxygène, deux réactions sont dominantes :
C + 16O16O ® C16O16O de
cte cinétique nommée K16
C + 16O18O ® C16O18O de
cte cinétique nommée K18
Et l’on peut
montrer, connaissant les concentrations deux molécules isotopiques des réactifs
et des produits que le coefficient de fractionnement isotopique cinétique de
réaction est de la forme a = (K18/K16)
Ce coefficient de fractionnement cinétique est-il lui aussi indépendant de la température ? La différence de réactivité des molécules isotopiques provient de différences de vitesse, donc d’énergie, donc de la température ? A priori, la température devrait favoriser le fractionnement, mais l’échange isotopique est lui aussi un processus cinétique favorisé par la température. Ce double processus se traduit par une courbe « Fractionnement versus température » en cloche ; dans un domaine de relativement basse température, une élévation de la température augmente le fractionnement jusqu’à un maximum ; au-delà l’échange devient dominant conduit vers un fractionnement de plus en plus faible. Pour l’heure, nous ne disposons pas d’une expression générale décrivant cette compétition des deux processus.
Lors des
transferts du minéral vers le vivant les processus biologiques opèrent aussi un
fractionnement qui favorise les isotopes légers. On observe ainsi un
enrichissement des plantes en
haut
retour
début
(Météorites Différenciées)![]() précédente page suivante
précédente page suivante ![]() (Météorites Indifférenciées)
(Météorites Indifférenciées)
plan