ENSM-SE / processus naturels /
terre_ronde
Retour

Trois
outils fondamentaux permettent d'imaginer l'intérieur de notre globe:
1 - un fil à plomb plus
un poids suspendu à un ressort, dans le champ de gravité;
2 - un stylet et un cylindre
à l'écoute d'une planète qui s'ébroue;
3 - une aiguille libre et
aimantée boussole dans le champ magnétique.
La
gravimétrie, en déterminant la direction et l'intensité de la pesanteur, résultante des accélérations
appliquées à un corps au repos dans le référentiel Terrestre, permet d'une
part de repérer des variations de densité (souvent utile dans la recherche minière), et d'autre part de
définir précisément les formes de
On
sait depuis 1687 avec Philosophiae Naturalis Principia Mathematica de I.
Newton que lorsque les pommes de masse m tombent, la force F qui les attire
vers
1 - Cavendish a mesuré la constante G, en 1798 à Paris.
1- Cavendish a mesuré la constante G, en 1798 à Paris
Son
dispositif expérimental (Fig. 1) comprenait deux petites masses égales,
suspendues en équilibre au bout d'un fil non torsadé. En approchant
symétriquement les 2 masses M, Cavendish provoque le rapprochement des masses
m: connaissant la distance entre les masses m et M, la force mise en jeu (celle
qu'il faut appliquer au dispositif, hors de la présence des masses M, pour
obtenir le même déplacement des masses m) Cavendish déduisit la valeur de
G= 6.67 10-11 SI (N.Kg-2.m2).
Dès lors, la masse de 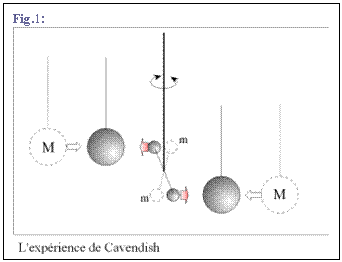 monochromatique) donne la valeur de
monochromatique) donne la valeur de
g=
G M / r2 (si
M=g.r2/G. = 5.976 1024Kg
Connaissant le volume de la terre on
en déduit alors une masse volumique
moyenne pour
Or AUCUNE
roche ordinaire échantillonnée à la surface du globe ne possède un poids
volumique dépassant
Le globe terrestre est donc constitué de 2 couches au
moins
Les masses volumiques de ces enveloppes sont très différentes.
Nombre d'observations directes ou indirectes suggèrent que
1) la nature des météorites
différenciées, soit ferreuses soit silicatées, qui suggère que la séparation
(partielle) du fer soit un phénomène courant dans les objets rocheux solaires;
2) la structure sismique de
3) la concentration en fer du
manteau, faible par rapport à celle des météorites indifférenciées, qui suggère
une redistribution du fer dans
On peut évaluer sommairement les densités et les rayons respectifs
du noyau dense et du manteau silicaté en se basant sur trois contraintes:
1) la masse de
2) la différence entre le moment
d'inertie réel du globe terrestre (= 0.33.MR2) et celui d'un globe
homogène (0.4 MR2 )
3) le poids volumique du
manteau, qui est au minimum celui des roches connues du manteau supérieur, rmanteau =3.3 kg.dm3;
le poids volumique du noyau rnoyau, est inconnu.
 On écrit alors la relation liant les poids volumiques de
On écrit alors la relation liant les poids volumiques de
r moy = rmanteau+ (rnoyau-rmanteau)(Rnoyau/RTerre)3
et celle liant les moments réel et théorique,
0.331rmoy = 0.4[rmanteau+ (rnoyau-rmanteau)(Rnoyau/RTerre)5]
on en tire une relation entre le rapport des poids volumiques rnoyau / rmanteau et le rapport des rayons RR
= Rnoyau/RTerre telle que:
rmanteau+ (rnoyau-rmanteau)(Rnoyau/RTerre)3
= 0.4/0.331 [rmanteau+ (rnoyau-rmanteau)(Rnoyau/RTerre)5]
avec r =(rnoyau rmanteau) et
RR = Rnoyau/RTerre on a:
rmanteau + r.RR3 = 1.21 rmanteau+ 1.21r.RR5
r
= 0.21 rmanteau /(RR3-1.21RR5)
En
clair, rnoyau-rmanteau = 0.21 rmanteau /(RR3-1.21RR5)
et rnoyau / rmanteau = 1+ 0.21/(RR3-1.21RR5)
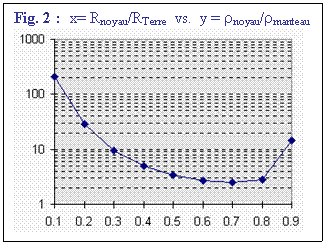
Le diagramme joint (Fig. 2) montre que rnoyau / est au
moins égal à 2.5rmanteau. Pour un
noyau situé à
2- La
mesure de la pesanteur
La pesanteur au point P
considéré, appliquée à une masse unité m, est définie comme la résultante des
accélérations appliquées à m, corps au repos dans le référentiel Terrestre. Cette
pesanteur peut être représentée en tout point autour de P par un ensemble de
vecteurs g®, définis en sens direction et intensité, ensemble que l'on
appelle champ de gravité.
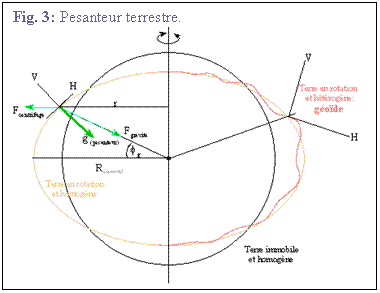
La pesanteur est composée de
3 termes (Fig.3):
1 - la gravité
terrestre (Fg=mg) avec g=
G.M/r2 »
2 - la force centrifuge (Fc
= m.w2r » m.w2R.cosf );
3 - l'attraction du reste
de l'univers non figurée ici (< 1 mgal), qui exerce des forces de marées
(de l'ordre de 20cm pour les marées terrestres) souvent négligées.
Les conséquences en sont :
1 - le fil à plomb (g) ne passe pas par le centre de
2 - l'intensité du champ de pesanteur varie
avec la latitude.

Une Terre qui tourne, si elle se comporte comme un fluide, peut
être considérée comme un ellipsoïde de révolution. Les mesures de méridiens
(Fig. 4), effectuées au XVIII° au pôle et à l'équateur, aboutirent à une valeur
estimée de 1/280 à 1/266. La valeur adoptée vers 1950, avant le 1° Spoutnik,
était de 1/297 (H. Jeffreys). Avec Spoutnik-2 King-Hele révise sa valeur en
1957 (1/298), très proche de la valeur admise de nos jours, 1/298.25.
En outre, les paramètres locaux viennent encore perturber la
pesanteur:
1 - l'altitude, en
accroissant la distance au centre de
2 - La topographie,
en introduisant des excès ou des déficits dans les masses environnantes,
modifie la direction et l'intensité de la pesanteur. (Fig. 5).
On comprend donc dès lors, que pour être intelligible, toute
mesure du champ de pesanteur doit être rapportée à une surface de référence. On
utilise internationalement l'ellipsoïde de référence nommé «ellipsoïde de Hayford»
dont l'aplatissement est de 1/298.25.
Il faut donc corriger la valeur mesurée en chaque point (Fig. 6)
la valeur g0 = g »
1 - par une correction de latitude qui tient compte
de la force centrifuge, soit
gt » 978.033 +(1 +0.005.sin2f-0.000006 sin2.2f), la parenthèse est nulle à l'équateur, qui nous donne la valeur théorique de la pesanteur à la latitude
f, point de mesure.
2 - on introduit
une correction dite “ à l'air libre ” ou de Faye
ou correction d'altitude, faite en supposant qu'il n'y a que de l'air
entre le point de mesure et le géoïde (Fig. 6);
Elle est égale à (dg/dz) h
avec un gradient vertical de gravité (dg/dz) = 0.309 mgal m-1 et h
l'altitude au dessus de l'éllipsoide.
on appelle anomalie à l'air
libre (FA) la différence entre la valeur mesurée gmes corrigée de
l'altitude au dessus de l'ellipsoide et la valeur théorique en ce point de
l'ellipsoide
FA = [gmes + (dg/dz) h] - gt. Elle ne dépasse pas 100 mgals en valeur absolue, et met en
évidence un déficit de masse au droit des fosses océaniques et inversement un
excédent au droit des chaînes de montagne, avec un couple négatif positif très
net au niveau des zones de subduction.
3 - on opère enfin
les 2 corrections de Bouguer,
a) la correction dite
“ de plateau ”, qui prend
en compte l'attraction des masses comprises entre le point considéré et le
géoïde de façon homogène, et
b) la correction dite
“ topographique ” qui
tient compte de la répartition des reliefs.
On appelle finalement anomalie de Bouguer, l'écart entre la pesanteur théorique calculée au point considéré
sur l'ellipsoïde de référence, et la pesanteur mesurée et corrigée.


3-
Isostasie: comportement hydrostatique de la lithosphère
L’écart
entre la pesanteur théorique calculée et la pesanteur mesurée et corrigée peut
être fort, de l'ordre de - 300 à + 300 mgal. Il est négatif au droit des
chaînes de montagnes et positif au droit des océans. Tout se passe donc comme
si le calcul de la réduction de Bouguer était largement inutile et que l'excès
de masse que crée le relief montagneux au-dessus du géoïde était déjà quasi
compensé (avant toute correction) en dessous de la surface de référence
choisie, la correction introduisant alors un «déficit» apparent de masse. Cette
anomalie<0 résulte donc largement du calcul de correction lui-même et le
poids d'une colonne de terrain apparaît finalement constant d'une verticale à
l'autre. Il s'opère donc, d'une verticale à l'autre, une compensation de type hydrostatique, appelée isostasie.
Plusieurs
modèles ont vu le jour (Fig. 7). Tous admettent que la croûte, rigide et
moins dense que le manteau fluide, flotte sur celui-ci (Archimède). L'équilibre
des poids des différentes colonnes de terrain est donc parfaitement réalisé
au-delà d'une certaine profondeur, dite de compensation. Le modèle de Pratt, à la fin du siècle dernier,
mettait en jeu des colonnes de terrain de densités différentes, donc
d'épaisseurs différentes. Celui de Airy,
quelques années plus tard, mettait en jeu des colonnes de même densité
discrétisant une couche homogène. Enfin, le modèle de Vening Meinesz, datant du milieu du XX°, s'appuie sur le fait
que la réponse élastique de la croûte
est d'une amplitude beaucoup plus importante que la dimension des reliefs
qu'elle porte. Autrement dit, la compensation isostatique d'un relief est
régionale.
L'influence
des racines peut être exprimée par une nouvelle correction, dite
“ isostatique ”. Toutefois, l'existence d'anomalies résiduelles montre
que l'équilibre n'est pas réalisé partout. La cause en est la viscosité très
élevée du manteau qui implique un temps de réponse important à toute
modification de l'équilibre. Ainsi, le bouclier Baltique remonte encore de nos
jours alors qu'il est allégé depuis 10 000 ans environ du poids des glaces qui
le couvraient.
Le
premier enseignement essentiel de la gravimétrie est donc la confirmation de la
plasticité de


On
appelle géoïde la surface équipotentielle
de pesanteur coïncidant avec le niveau moyen des mers, prolongée à travers les
continents. Si
En
fait,
4-
Géodésie satellitaire
a) Les satellites artificiels
ont été utilisés de 2 façons: en mode passif, le satellite servit tout d'abord
de réflecteur, la télémétrie laser apportant dans les années 60 une précision
de la mesure de la position instantanée du satellite de l'ordre du mètre; en
géodésie dynamique, l'objectif est de déterminer le mouvement du satellite par
comparaison des données de poursuite avec la trajectoire théorique, modèle
calculé à partir des équations de la mécanique Newtonienne. Les données
accessibles sont de 3 types: 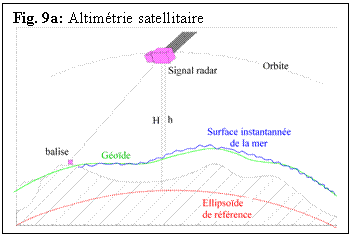 mesures de distance (télémétrie laser, Fig. 9a)
mesures de distance (télémétrie laser, Fig. 9a)
b) mesures de vitesse (effet
Doppler)
c) mesures angulaires
(photographies sur fond d'étoiles)
d) La modélisation de la
trajectoire nécessite de connaître les paramètres suivants:
e) la position des stations de
mesure au sol;
f)
le champ de pesanteur;
g) le freinage lié à l'atmosphère;
h) la pression du vent solaire;
i)
les déformations de
j)
le mouvement de l'axe de rotation de
k) l'attraction de l'ensemble
des planètes du système solaire.
 Aucun paramètre n'est connu
parfaitement, et la géodésie dynamique consiste donc à opérer un ajustement
itératif des données au modèle théorique. L'utilisation conjointe de plusieurs
satellites sur près de 30 années a permis de proposer des modèles de plus en
plus affinés du champ de la pesanteur terrestre. L'analyse de la trajectoire
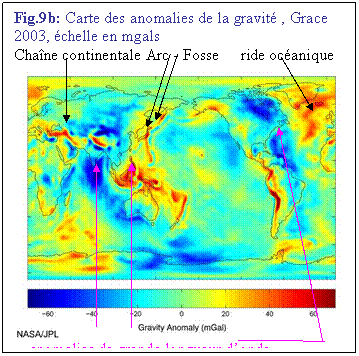
des satellites fournit une image très précise du géoïde (Fig. 9). En
effet, les ondulations du géoïde à l'échelle de la centaine de km (flèches
noires) traduisent très fidèlement la topographie car la compensation
isostatique d'une chaîne ou d’une fosse sous-marine par exemple, dépasse largement
la surface occupée par la chaîne ou la fosse. Il s'ensuit donc un excès de
masse local (au droit de la chaîne) ou un déficit local (au droit de la fosse),
qui implique un éloignement du géoïde (vers le haut pour la chaîne).
Aucun paramètre n'est connu
parfaitement, et la géodésie dynamique consiste donc à opérer un ajustement
itératif des données au modèle théorique. L'utilisation conjointe de plusieurs
satellites sur près de 30 années a permis de proposer des modèles de plus en
plus affinés du champ de la pesanteur terrestre. L'analyse de la trajectoire
des satellites fournit une image très précise du géoïde (Fig. 9). En
effet, les ondulations du géoïde à l'échelle de la centaine de km (flèches
noires) traduisent très fidèlement la topographie car la compensation
isostatique d'une chaîne ou d’une fosse sous-marine par exemple, dépasse largement
la surface occupée par la chaîne ou la fosse. Il s'ensuit donc un excès de
masse local (au droit de la chaîne) ou un déficit local (au droit de la fosse),
qui implique un éloignement du géoïde (vers le haut pour la chaîne).
La figure 10 met
en évidence d'une part le bourrelet équatorial (aplatissement polaire) et
d'autre part les creux et bosses du géoïde à grande longueur d’onde (en violet
dans la figure 9). La déformation maximum, très exagérée sur la figure, est en
fait inférieure à
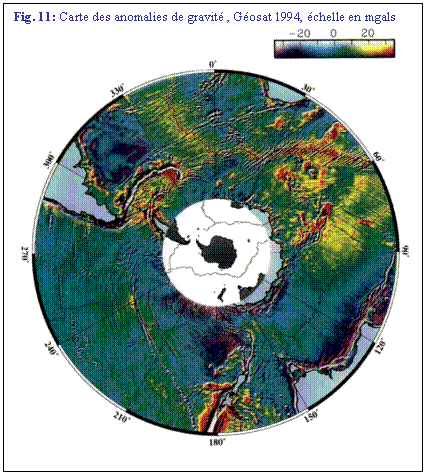
Inversement, tout les types
de structures à petite échelle sont remarquablement identifiables sur les
figures 9 et/ou 11:
l)
dorsales chaudes Sud-Atlantique et Indien;
m)
dorsale froide Nord-Atlantique
n)
failles transformantes mettant en regard deux compartiments d'âges
variés (et donc de structure thermique différente);
o)
chaînes sous-marines de points chauds
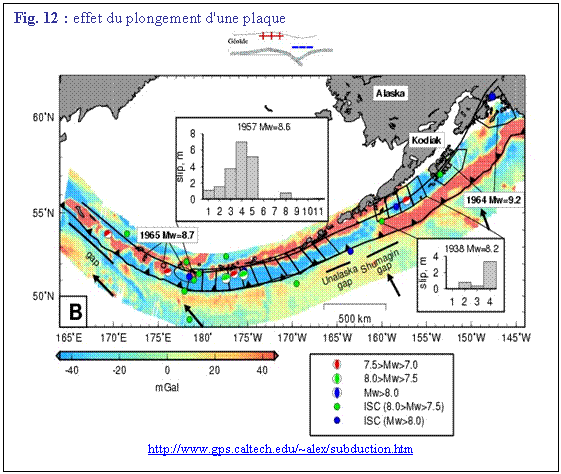
p)
fosses océaniques, qui provoquent un déficit local de masse
encadré par deux anomalies, celle bien marquée (en rouge) de l’arc et celle
moins marquée (en jaune) du côté océanique qui souligne le ploiement de la
plaque subductée (Fig. 12).
q) Chaîne de collision (Alpes
Himalaya)
r)
chaînes surmontant une zone de subduction (marges actives = Andes
et Rocheuses)
Fig. 10: le géoïde terrestre http://principles.ou.edu/earth_figure_gravity/geoid/index.htm

haut
retour
début
(
WEB chp2 )
![]() précédente page suivante
précédente page suivante ![]() ( Séismicité )
( Séismicité )
plan