ENSM-SE / processus
naturels / terre_ronde
Les
enveloppes rocheuses de
Retour
Les météorites précoces formées dans la nébuleuse solaire (les
chondrites CI) et la photosphère solaire actuelle nous enseignent qu’au moment
de la formation de
Partant des proportions
massiques des éléments majeurs du manteau:
O=50%;
Si=22% ; Mg=22% ; Fe=6% e : Mg=22%, Fe=6%
et des masses molaires
des éléments :
mO=16, mSi=28, mMg=24.3, mFe=56
on constate que le rapport molaire du manteau Fe/Mg = (6/56)
/ (22/24.3) n’est que de 0.1 environ. A Magnésium constant, il manque donc une
quantité importante de Fer dans le manteau que nous pouvons essayer
d’estimer :
1- la masse molaire moyenne
du manteau (0.5*16 + 0.22*28 + 0.22*24.3 + 0.06*56) est de =22.8.
2- le nombre de moles de
Magnésium NMg dans le manteau s'écrit : NMg = Mg/mMg
* Mmanteau (1)
Si
l'on suppose que le rapport molaire Fe/Mg de 
la masse manquante de fer est :
on sait que
Or, puisque Mg est
constant, on a
donc on réécrit la masse
manquante de fer du manteau
et en remplaçant de (1) NMg par Mg/mMg
* Mmanteau on a :
ou
La
masse manquante de fer représenterait donc environ 40% de la masse du manteau.
Or, le rapport des masses entre le noyau ferreux et manteau est de 0.48 et non 0.4.
Mais le fer n’est pas le seul élément contenu dans le noyau ; à partir de
la composition des sidérites et en raison des contraintes imposées par la
géophysique on estime que le noyau est aussi constitué de nickel en faible %,
et d'éléments légers (O, Si, ou S). D’après Allègre et al., 1995,
la composition du noyau serait la suivante : Fe=79%, Ni=5%, Si=7%, S=2%,
O=4%. Sa densité doit être comprise entre 10 et 12, et il est conducteur de l’électricité.
1 - Le noyau liquide
Sismiquement
transparent pour les ondes S et ralentissant fortement les ondes P, le noyau
terrestre est à l'état liquide (Chp. 3.B.4.d).
La pression varie de 
environ d’éléments légers, on obtient une température de
l’ordre de 5000°K. Considérant alors
que la chaleur du noyau liquide est transportée par convection, le gradient
adiabatique donne pour la surface du
noyau une température de l’ordre de 3800°K. La température au centre de
On
estime que la viscosité du fer fondu dans les conditions régnant dans le noyau
est peu différente de celle que l'on obtient en surface. Elle serait donc du
même ordre de grandeur que la viscosité de l'eau ! Nous avons vu au
chapitre précédent que le Noyau fonctionne comme une magnétohydrodynamique et
que la force de Coriolis joue un rôle important dans le développement de ce
champ.
On
sait que Coriolis n’est applicable qu’à un objet animé d’une vitesse
significative. Dans le noyau, les vitesses de déplacement par convection
seraient de l’ordre de une à plusieurs dizaines de kilomètres par an.
« Dynamo », le modèle de convection sphérique en rotation et de
calcul du champ (dipolaire et non dipolaire) de Glatzmaier et Roberts
(1997 ; Fig. 1, et copie de l’animation du modèle) intégrant le rôle de
la graine solide conductrice, montre de larges courants équatoriaux, tournant
vers l’est au voisinage de la graine et vers l’ouest à proximité du manteau. Le
champ magnétique simulé est majoritairement dipolaire (Fig. 2). Une
transition apparaît à la limite noyau-manteau, séparant un champ à structure
complexe produit par le noyau liquide du reste du champ beaucoup plus régulier.
Les structures non dipôles obtenues par ce modèle se décalent lentement vers
l’ouest de 2°/an, suggérant que la graine tourne légèrement plus vite que le
manteau terrestre. Pour Ken Creager ce différentiel de
vitesse pourrait être très petit <0.5°.
2 - La graine solide
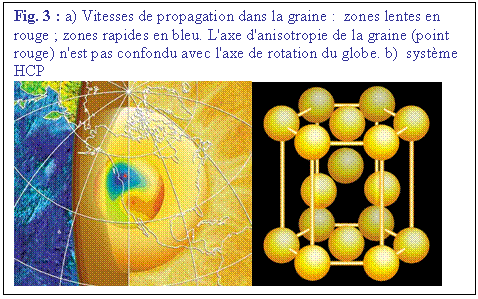Nous avons vu que la vitesse de transmission des rais
sismiques présente une zone interne plus rapide que son enveloppe plus lente. A
la fin des années 90, W.J. Su et A.M. Dziewonski ont
découvert en analysant précisément la distribution spatiale des vitesses des
ondes sismiques que la graine présente en outre un axe d'anisotropie incliné
d'une dizaine de degrés par rapport à l'axe de rotation de
1 - soit une convection
axisymétrique provoquant une orientation des cristaux de fer ;
2 - soit un dépôt orienté de
ces mêmes cristaux par le champ magnétique du noyau.
Dans les deux cas,
l’anisotropie observée résulterait du mode de cristallisation du fer sous haute
pression, stable dans le système hexagonal compact (HCP, Fig. 3b),
axisymétrique. L'orientation préférentielle des cristaux peut engendrer des
variations fortes des propriétés élastiques selon les directions. Pour S.I.
Karato (1999), cette anisotropie serait provoquée par les forces de
Lorenz liées au champ toroïdal qui, en comprimant de plus en plus la graine (en
direction de l’axe de rotation) depuis l’équateur (où la force est nulle
puisque les lignes du champ changent de sens) vers le pôle de la graine (où les
forces de Lorenz deviennent maximum). En observant le comportement de rais
sismiques répétés au cours des 30 dernières années, couplant une même région
sismiquement active avec un ou des observatoires de mesure, X.
Song et P. Richards ont mis en
évidence une évolution temporelle de l’axe d'anisotropie de la graine,
traduisant une rotation de la graine vers l’ouest de 1° par an. Le mécanisme et
l’ampleur de cette super-rotation de la graine par rapport au manteau, et son
existence même, sont encore largement débattus. Pour Kenneth Creager,
cette super rotation serait due au mécanisme complexe de transfert
d’énergie du noyau vers le manteau, dont le modèle très fertile de géodynamo de
Glatzmaier et Roberts donne l’image suivante : le champ magnétique généré
dans
Il convient cependant de rester critique, d'abord parce que
les données collectées sont limitées dans le temps et donc ne couvrent qu'une
fraction très petite de révolution de la graine, et ensuite parce que les
données les plus anciennes (années 60) sont à la fois moins précises et moins
nombreuses. Ainsi, l'apparente inclinaison de l'axe d'anisotropie pourrait
provenir de la distribution irrégulière des stations sismologiques et des
séismes observés (principalement issus de rides océaniques et de zones de
subductions). En outre, selon S. Tanaka et H. Hamaguchi (1997) il
est possible que la graine ne soit pas de symétrie cylindrique. De plus, comme
le souligne Annie Souriaux, la rotation différentielle de la
graine pose un problème théorique: la forme de la graine doit être modelée par
le champ de gravité du manteau. Celui-ci étant hétérogène il génère
nécessairement des creux et des bosses à la surface de la graine. Si celle-ci
est bien en super rotation par rapport au manteau, leur couplage gravifique
doit engendrer la disparition et la recréation simultanée de ces creux et
bosses (de quelques x100m tout de même)… En d’autres termes, si la graine
tourne plus vite que le manteau, elle doit adapter sa forme au champ de
gravité. Il faut donc que les "bosses" de la graine fondent pour se
recristalliser ailleurs, ou se déforment
par viscosité. Pour Laske et Masters (1999), cette super rotation
n’existerait pas, et ne serait qu’un artefact lié justement aux hétérogénéités
de la graine. Le noyau recèle encore bien des mystères !
Il est à noter que parmi
les champs magnétiques des planètes du système solaire, seuls les champs actifs
ont une forte intensité (tab. 1 du Chp. 3). Depuis, d'autres analyses
ont conduit à des valeurs allant On constate aussi (Fig. 4) que si
l’orientation du champ dipolaire est souvent proche de l’axe de rotation de la
planète, Uranus et Neptune montrent un champ d’orientation très différente. La
nature de ces champs n’est pas encore bien connue. Constituée de fer quasi pur,
la graine résulte de la cristallisation du noyau. Les calculs laissent à penser
que 30 à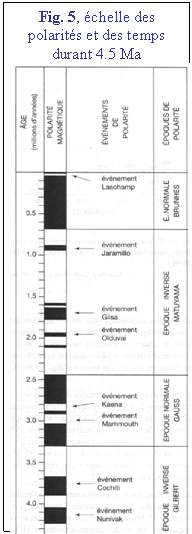 
la surface du noyau, libérant de l'énergie potentielle de
gravité. L'ensemble pourrait suffire, même sans radioactivité (40K,
§ bilans énergétiques), à entretenir la géodynamo. Une telle géodynamo peut fonctionner
dès lors que le noyau existe, ce qui expliquerait que l’on ait pu observer
l'existence de ce champ dans des roches très anciennes, allant jusqu'à 3.8 Ga.
(Ishua, Groenland) et même 3.96 Ga. (Acasta, USA). En cas d'arrêt de la
convection dans le noyau, on estime à 10 000 ans environ le temps de
disparition du champ magnétique. Ce temps correspond à la dissipation par effet
Joule de l'énergie disponible dans le fluide conducteur arrêté.
3 - Les inversions du champ terrestre
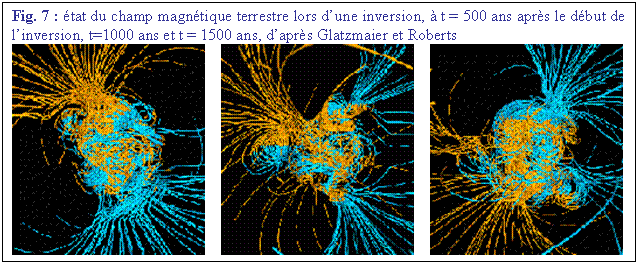Les inversions
du champ terrestre sont fréquentes. La durée moyenne de stabilité est de
l'ordre de quelques centaines de milliers d'années, mais elle peut être
beaucoup plus courte (Fig. 5). Inversement, par deux fois au moins
(Fig. 6), au Permien (limite
Permien-Trias = 250 Ma.) et au Crétacé (Limite Crétacé-Tertiaire =65 Ma.), la géodynamo a
“ oublié ” de permuter ses pôles pendant plusieurs dizaines de
millions d'années. Les inversions bien documentées du paléo champ de
haut
retour
début
précédent chapitre suivant 
( WEB Chp 3 )
précédente page suivante 
( Couche D’’ )
plan